Continuidad

Intuitivamente, la continuidad significa que un pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de curva.

Una función es continua en un punto si existe límite en él y coincide con el valor que toma la función en ese punto.

Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin levantar el lápiz de la hoja de papel.

En los casos que una función es continua, las condiciones que se deben cumplir son:
1) la imagen de f(a) existe
2) Lim x→a existe
3) f(a)= Lim x→a.





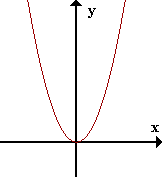
f(x)=x2

Una función f(x) es continua en un punto a si lim f(x) = f(a).

                                                                         x→a

Nota: observar que debe existir f(a) y debe existir el limx->a f(x) y debe ser igual a f(a).

Ejemplo de discontinuidad

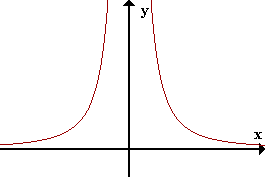
f(x)= 

1/x²

Discontinua en x=0 (No existe f(0))

Fuentes: 

http://matematica.50webs.com/continuidad.html

http://darkcity2111.wordpress.com/3-8-funciones-continuas-y-descontinuas-en-un-punto-y-en-un-intervalo/

http://aula.tareasplus.com/Roberto-Cuartas/Calculo-Diferencial/Continuidad-de-una-funcion-en-un-punto-parte-1

Tipos de limites

Los limites infinitos en un punto finito: En la situación del dibujo, se dice que el limite cuando "x"

se acerca por la derecha de "a" es "+∞", pues a medida que la "x" se acerca a a, la funcion se hace

cada vez mayor:

lım f(x)=+∞

                                                             x→a

(de igual forma se puede definir cuando nos acercamos por la izquierda.)

Límites finitos en el infinito: Se dice que una función tiene límite "b" cuando "x" tiende a "+∞"
cuando la función se acerca a "b" cuando la "x" se hace cada vez mayor, es decir:

lım f(x) = b

                                                             x→∞

Gráficamente: 

Límites infinitos en el infinito: Aparece este caso cuando si "x" tiende a "+∞" la función se hace

cada vez mayor o menor (lo mismo si "x" tiende a "−∞").

Un ejemplo gráfico de este tipo de límites sería:

En este caso:

lım f(x) = −∞

                                                            x→∞

Fuentes: http://sauce.pntic.mec.es/~jpeo0002/Archivos/PDF/T09.pdf

Límites

El límite es muy importante a la hora de estudiar funciones porque nos introduce al mundo del “cálculo infinitesimal”, una herramienta muy importante tanto para las matemáticas como para la física. Cuando calculo el límite lo que quiero averiguar es a qué valor tiende el valor de una función. El límite es siempre una tendencia: x sólo se acerca al valor al que tiende pero nunca puede ser él mismo.

En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. El límite de una función es un concepto fundamental del cálculo diferencial matemático.

Por definición intuitiva podemos entender que el de limite de "f(x)" cuando "x" tiende a "c", es una constante "L":

lim f(x)= L

                                                               x→c

Un limite se puede entender como el espacio que hay entre dos puntos o como la cercanía que existe hacia un valor sin llegar a él.

Muchas veces, una función puede no estar definida en un punto, pero podemos pensar a qué valor se aproxima la función mientras se acerca más y más a ese punto (eso es el límite).






Fuentes:
http://www.aula365.com/post/limites/
https://es.khanacademy.org/math/differential-calculus/limits_topic