Hay bastantes tipos de ejemplos de aplicación de máximos y mínimos en la vida real. Un clásico es el de construir con determinada cantidad de material, un recipiente de volumen máximo.
Por ejemplo, si deseas cercar un terreno, pero solo posees una determinada longitud de valla, puedes utilizar los máximos y mínimos para que, con esa longitud de valla, puedas cubrir la mayor cantidad de área.
Los máximos y mínimos tienen un gran significado en el mundo de los negocios. Todas las empresas utilizan las funciones de máximos para sus beneficios, ventas y ganancias y las de mínimos para acortar costos y pérdidas.
Fuentes:
http://www.ehowenespanol.com/resumen-aplicaciones-maximos-minimos-negocios-info_273705/
lunes, 1 de diciembre de 2014
Resolución de máximos y mínimos
1. Hallamos la derivada primera y calculamos sus raíces.
f'(x) = 3x^2 − 3 = 0
x = −1 x = 1.
2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella los ceros de derivada primera y si:
f''(x) > 0 Tenemos un mínimo.
f''(x) < 0 Tenemos un máximo.
f''(x) = 6x
f''(−1) = −6 Máximo
f'' (1) = 6 Mínimo
3. Calculamos la imagen (en la función) de los extremos relativos.
f(−1) = (−1)^3 − 3(−1) + 2 = 4
f(1) = (1)3 − 3(1) + 2 = 0
Máximo(−1, 4) Mínimo(1, 0)
Fuentes:
http://www.dervor.com/derivadas/maximos_mimimos.html
f'(x) = 3x^2 − 3 = 0
x = −1 x = 1.
2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella los ceros de derivada primera y si:
f''(x) > 0 Tenemos un mínimo.
f''(x) < 0 Tenemos un máximo.
f''(x) = 6x
f''(−1) = −6 Máximo
f'' (1) = 6 Mínimo
3. Calculamos la imagen (en la función) de los extremos relativos.
f(−1) = (−1)^3 − 3(−1) + 2 = 4
f(1) = (1)3 − 3(1) + 2 = 0
Máximo(−1, 4) Mínimo(1, 0)
Fuentes:
http://www.dervor.com/derivadas/maximos_mimimos.html
Criterios de la primera y segunda derivada
Criterio de la primer derivada:
La base del presente criterio radica en observar que los máximos o mínimos locales son consecuencia de observar los siguientes hechos:
La base del presente criterio radica en observar que los máximos o mínimos locales son consecuencia de observar los siguientes hechos:
- Cuando la derivada es positiva la función crece.
- Cuando la derivada es negativa la función decrece.
- Cuando la derivada es cero la función tiene un máximo o un mínimo.
Sea f(x) una función y c un número en su dominio. Supongamos que existe a y b con a<c<b tales que:
1.- f es continua en el intervalo abierto (a,b) (de acuerdo con el teorema de Rolle)
2.- f es derivable en el intervalo abierto (a,b), excepto quizá en c;
3.- f´(x) es positiva para todo x<c en el intervalo y negativa para todo x>c en el intervalo.
Entonces f tiene un máximo local en c.
Criterio de la segunda derivada:
Sea f una función con su primera derivada definida, al menos, en un intervalo abierto conteniendo al número a. Si f´´ esta definida entonces podemos considerar los siguiente aspectos:
a).- Si f´(a)=0 y f´´(a)<0 entonces se dice que f tiene un máximo local en a.
b).- Si f´(a)=0 y f´(a)>0 entonces se dice que f tiene un mínimo local en a.
Fuentes:
Sentido de concavidad
- Una función es cóncava en un intervalo de su dominio cuando:
Dados dos puntos cualesquiera de dicho intervalo x1 y x2, el segmento que une los puntos (x1, f(x1)) y (x2, f(x2)) siempre queda por debajo de la gráfica.
- Una función es convexa en un intervalo de su dominio cuando:
Dados dos puntos cualesquiera de dicho intervalo x1 y x2, el segmento que une los puntos (x1, f(x1)) y (x2, f(x2)) siempre queda por encima de la gráfica.
Fuentes:
http://www.vitutor.com/fun/5/c_10.html
Valores críticos
Determinar los puntos críticos consiste en hallar los valores extremos de la función, estos valores extremos son los puntos más altos y más bajos de la gráfica de una función y una de las herramientas para su determinación es aplicando la derivada.
Fuentes:
https://sites.google.com/site/sarahyjoffrecalculo/home/unidad-iii/3-1-puntos-criticos-y-valores-extremos/3-1-2-maximos-y-minimos
http://calculo-maximosyminimos.blogspot.mx/
Fuentes:
https://sites.google.com/site/sarahyjoffrecalculo/home/unidad-iii/3-1-puntos-criticos-y-valores-extremos/3-1-2-maximos-y-minimos
http://calculo-maximosyminimos.blogspot.mx/
Punto de inflexión
El punto que, en una función continua, separa la parte convexa de la cóncava, se llama punto de inflexión de la función. En ellos la función no es cóncava ni convexa sino que hay cambio de concavidad a convexidad o al revés.
Los puntos de inflexión están caracterizados por:
TEOREMA
Sea y=f(x) la ecuación de una función.
Si f ''(a)=0, o f '' (a) no existe, y la derivada f '' (x) cambia de signo al pasar por el valor de x=a, entonces, el punto de la función de abscisa x=a es un punto de inflexión.
Ejemplo:
El punto x=1 es un punto de inflexión, puesto que antes de x=1 la derivada segunda es negativa (convexa) y después de x=1 es positiva (cóncava).
Fuentes:
http://thales.cica.es/rd/Recursos/rd99/ed99-0295-01/punto7/punto7.html
Los puntos de inflexión están caracterizados por:
TEOREMA
Sea y=f(x) la ecuación de una función.
Si f ''(a)=0, o f '' (a) no existe, y la derivada f '' (x) cambia de signo al pasar por el valor de x=a, entonces, el punto de la función de abscisa x=a es un punto de inflexión.
Ejemplo:
El punto x=1 es un punto de inflexión, puesto que antes de x=1 la derivada segunda es negativa (convexa) y después de x=1 es positiva (cóncava).
Fuentes:
http://thales.cica.es/rd/Recursos/rd99/ed99-0295-01/punto7/punto7.html
Máximos y mínimos
Máximo absoluto
Una función tiene su máximo absoluto en x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.
Mínimo absoluto
Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.
Máximos y mínimos relativos
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.
Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.
Una función tiene su máximo absoluto en x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.
a=0
Mínimo absoluto
Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.
b=0
Máximos y mínimos relativos
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.
Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.
sábado, 29 de noviembre de 2014
Usos y aplicaciones de derivadas
La derivada es la tasa de cambio, así que podemos hallar la velocidad(Siendo esta la primera derivada) y la aceleración(Siendo esta la segunda derivada) de algún objeto.
También tenemos la razón de cambio. Podemos hallar la velocidad de cambio de algo, como cuan rápido se vierte un liquido en algún recipiente, o la velocidad de movimiento.
La derivada permite ver, a través de la pendiente en todo punto de la curva, la evolución o el cambio de muchos fenómenos físicos. Permite calcular los puntos clave, ahí donde la pendiente es 0 (máximos y mínimos) para buscar los óptimos, por ejemplo, permite hacer otros muchos cálculos asociados a este hecho de la pendiente de la tangente en cada punto de la curva.
En física, electricidad, electrónica, en química, permite estudiar muchos fenómenos evolutivos asociados como la velocidad, la aceleración, los flujos, las acumulaciones. Las derivadas están siempre presentes. Se utiliza en economía, se utiliza en gestión, se utiliza en arquitectura. Los sistemas de cálculo de frenado y de automatización utilizan derivadas, los sistemas y las máquinas automatizadas para fabricar o para controlar utilizan derivadas.
Por ejemplo, los sistemas que controlan la parada de el ascensor para que ésta sea suave, se controla el “jerk” que es la derivada de la aceleración con relación al tiempo.
Fuentes:
http://www.incress.com/valores-participacion/2012/07/28/%C2%BFque-es-y-para-que-sirve-una-derivada/
También tenemos la razón de cambio. Podemos hallar la velocidad de cambio de algo, como cuan rápido se vierte un liquido en algún recipiente, o la velocidad de movimiento.
La derivada permite ver, a través de la pendiente en todo punto de la curva, la evolución o el cambio de muchos fenómenos físicos. Permite calcular los puntos clave, ahí donde la pendiente es 0 (máximos y mínimos) para buscar los óptimos, por ejemplo, permite hacer otros muchos cálculos asociados a este hecho de la pendiente de la tangente en cada punto de la curva.
En física, electricidad, electrónica, en química, permite estudiar muchos fenómenos evolutivos asociados como la velocidad, la aceleración, los flujos, las acumulaciones. Las derivadas están siempre presentes. Se utiliza en economía, se utiliza en gestión, se utiliza en arquitectura. Los sistemas de cálculo de frenado y de automatización utilizan derivadas, los sistemas y las máquinas automatizadas para fabricar o para controlar utilizan derivadas.
Por ejemplo, los sistemas que controlan la parada de el ascensor para que ésta sea suave, se controla el “jerk” que es la derivada de la aceleración con relación al tiempo.
Fuentes:
http://www.incress.com/valores-participacion/2012/07/28/%C2%BFque-es-y-para-que-sirve-una-derivada/
Reglas de derivación de funciones trascendentes
Trigonométricas:
- La derivada de Seno:
- La derivada de Coseno:
- La derivada de Tangente:
- La derivada de Cotangente:
- La derivada de Secante:
- La derivada de Cosecante:
Exponencial:
lunes, 10 de noviembre de 2014
Reglas de derivación de funciones algebráicas
1) Derivada de una constante:
y=c y'=0
Ejemplo:
2) Derivada de una variable:
y=x y'= 1
Ejemplo:
3)Derivada del producto de una constante por una variable:
y=cx y'= c
Ejemplo:
4) Derivada de una potencia:
Ejemplo:
5)Derivada de una función elevada a una potencia:

Ejemplo:
6)Derivada de una raíz:

Ejemplo:
7)Derivada de una suma de funciones:
8)Derivada del producto de dos funciones:
9)Derivada de la división de dos funciones (Cociente):
Ejemplo:
y=c y'=0
Ejemplo:
2) Derivada de una variable:
y=x y'= 1
Ejemplo:
3)Derivada del producto de una constante por una variable:
y=cx y'= c
Ejemplo:
4) Derivada de una potencia:
Ejemplo:
5)Derivada de una función elevada a una potencia:

Ejemplo:
6)Derivada de una raíz:

Ejemplo:
7)Derivada de una suma de funciones:
Ejemplo:
8)Derivada del producto de dos funciones:
Ejemplo:
9)Derivada de la división de dos funciones (Cociente):
Ejemplo:
Derivación aplicando la regla de los cuatro pasos
Razón de cambio
En la vida diaria se determinan razones de cambio de diversas situaciones de tipo natural, económico, social, situaciones en las que nos interesa conocer cuál es el mínimo o máximo valor, como aumenta o disminuye ese valor, en un intervalo de tiempo específico.
La razón de cambio es la velocidad a la que cambia una ecuación.
Razón de cambio (de una variable respecto a otra) es la magnitud del cambio de una variable por unidad de cambio de la otra. (También se le llama tasa de cambio.) Si las variables no tienen ninguna dependencia la tasa de cambio es cero.
En general, en una relación funcional "y=f(x)", la razón de cambio de la variable dependiente y respecto a la independiente "x" se calcula mediante un proceso de límite --de la razón [f(x+t)−f(x)]/t, denominada cociente diferencial.
En sentido estricto entonces, la razón de cambio es el límite del cociente diferencial cuando "t" tiende a cero.
Razón de cambio promedio (pendiente):
Razón de cambio promedio para una función:
Razón de cambio como límite (fórmula):
Nota: puedes aplicar la regla de los cuatro pasos para resolver diversas funciones y obtener su respectiva derivada
Fuentes:
http://www.matetam.com/glosario/definicion/razon-cambio-una-variable-respecto-a-otra
http://mathematicas3.blogspot.mx/2010/05/16-razon-de-cambio-o-calculo.html
La razón de cambio es la velocidad a la que cambia una ecuación.
Razón de cambio (de una variable respecto a otra) es la magnitud del cambio de una variable por unidad de cambio de la otra. (También se le llama tasa de cambio.) Si las variables no tienen ninguna dependencia la tasa de cambio es cero.
En general, en una relación funcional "y=f(x)", la razón de cambio de la variable dependiente y respecto a la independiente "x" se calcula mediante un proceso de límite --de la razón [f(x+t)−f(x)]/t, denominada cociente diferencial.
En sentido estricto entonces, la razón de cambio es el límite del cociente diferencial cuando "t" tiende a cero.
Razón de cambio promedio (pendiente):
Razón de cambio promedio para una función:
Razón de cambio como límite (fórmula):
Nota: puedes aplicar la regla de los cuatro pasos para resolver diversas funciones y obtener su respectiva derivada
Fuentes:
http://www.matetam.com/glosario/definicion/razon-cambio-una-variable-respecto-a-otra
http://mathematicas3.blogspot.mx/2010/05/16-razon-de-cambio-o-calculo.html
domingo, 5 de octubre de 2014
Continuidad
Intuitivamente, la continuidad significa que un pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de curva.
Una función es continua en un punto si existe límite en él y coincide con el valor que toma la función en ese punto.
Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin levantar el lápiz de la hoja de papel.
En los casos que una función es continua, las condiciones que se deben cumplir son:
1) la imagen de f(a) existe
2) Lim x→a existe
3) f(a)= Lim x→a.
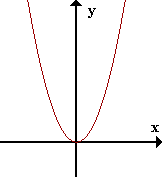
f(x)=x2
Una función es continua en un punto si existe límite en él y coincide con el valor que toma la función en ese punto.
Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin levantar el lápiz de la hoja de papel.
En los casos que una función es continua, las condiciones que se deben cumplir son:
1) la imagen de f(a) existe
2) Lim x→a existe
3) f(a)= Lim x→a.

f(x)=x2
Una función f(x) es continua en un punto a si lim f(x) = f(a).
x→a
Nota: observar que debe existir f(a) y debe existir el limx->a f(x) y debe ser igual a f(a).
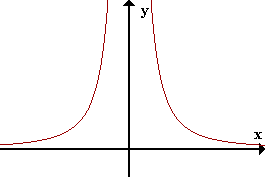
Ejemplo de discontinuidad

f(x)=
1/x²
Discontinua en x=0 (No existe f(0))
Fuentes:
Tipos de limites
Los limites infinitos en un punto finito: En la situación del dibujo, se dice que el limite cuando "x"
se acerca por la derecha de "a" es "+∞", pues a medida que la "x" se acerca a a, la funcion se hace
cada vez mayor:
lım f(x)=+∞
x→a
(de igual forma se puede definir cuando nos acercamos por la izquierda.)
cuando la función se acerca a "b" cuando la "x" se hace cada vez mayor, es decir:
lım f(x) = b
x→∞
Gráficamente:
Límites infinitos en el infinito: Aparece este caso cuando si "x" tiende a "+∞" la función se hace
cada vez mayor o menor (lo mismo si "x" tiende a "−∞").
Un ejemplo gráfico de este tipo de límites sería:
En este caso:
lım f(x) = −∞
x→∞
Suscribirse a:
Comentarios (Atom)

















 :
:


























